Conservación de la Energía
Parte 1
Parte 2
jueves, 13 de diciembre de 2012
martes, 6 de noviembre de 2012
miércoles, 3 de octubre de 2012
Condiciones de una ecuación diferencial lineal
Se dice que una ecuacion diferencial es lineal si la varianle dependiente y sus derivadas son de grado 1 y que estas no aparezcan como argumento ni como coeficiente.
Clasificación de las ecuaciones diferenciales
Dependiendo de la cantidad de variables independientes, respecto de las que se deriva:
Ordinarias: Una solo variable independiente.
Parciales: Dos o mas variables independientes.
POR ORDEN
El orden de la derivada mayor que existe en la ec. Diferencial, entiendase por orden a la cantidad de veces que se deriva una funcion ejemplo:
el orden es 3 puesto que la mayor de las derivadas es y“`.
POR GRADO
Es el grado de la derivada de mayor orden que existe en la ecuacion diferencial.Entiendase por grado la potencia a la que esta elevada la derivada. ejemplo:
el grado de esta ecs. es 2 ya que y“` esta elevada ala segunda potencia.
LINEALIDAD
Se dice que una ecuacion diferencial es lineal si la varianle dependiente y sus derivadas son de grado 1 y que estas no aparezcan como argumento ni como coeficiente.
Ejemplos de ecuaciones diferenciales
Algunos ejemplos clásicos de ecuaciones
diferenciales
a). Caída Libre
Denotemos con
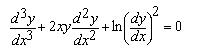
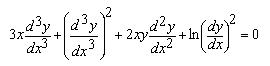
el espacio recorrido en el tiempo
por un cuerpo que cae libremente bajo la acción de la gravedad. Entonces
La ley de gravitación de Newton nos dice que
donde
denota la constante de gravitación universal. De (1.1.1) se deduce que
donde
es una constante. Si suponemos que en
la velocidad del cuerpo es conocida y denotada por
,
de (1.1.2) obtenemos que
De (1.1.3) obtenemos
donde
es una constante. Si suponemos que en
la posición del cuerpo es conocida y denotada por
,
de (1.1.4) obtenemos
La ecuación (1.1.5) representa la solución al problema de valor
inicial
Si en la ecuación (1.1.5) suponemos que
y por simplicidad
estamos ante el caso de caída libre y tendremos, por (1.1.3) y (1.1.5)
que
b) Caída con movimiento retardado.
Si suponemos que el aire ejerce una resistencia proporcional a la velocidad del cuerpo de masa
la segunda ley de Newton nos dice que
La ecuación (1.1.7) la escribimos así:
donde
Puesto que
(1.1.8) toma la forma
De (1.1.9) obtenemos que
para alguna constante
,
o también así
Si suponemos que
( el cuerpo parte del reposo) (1.1.10) toma la forma
De (1.1.11) se deduce que
ésto es, la velocidad de caída tiende a
estabilizarse.
c) Descomposición radactiva.
Si llamamos
la cantidad de material radiactivo que se descompone con el transcurso del
tiempo, la ecuación diferencial que rige dicha descomposición se
rige por medio del siguiente problema de valor inicial
donde
es una constante que depende del material que consideremos. El signo menos
indica que estamos ante un proceso de descomposición. Con
indicamos la cantidad de material con la que se inicia el proceso de
descomposición. La solución al problema (1.1.12) es
La vida media del material es el tiempo
necesario para que el material se reduzca a la mitad, ésto es
De (1.1.14) se deduce que
Observemos que la vida media
no depende de la cantidad inicial del material. Un gramo de plutonio y una
tonelada del mismo se reducen a su mitad en el mismo tiempo
Willard Libby descubrió en 1940 el radio carbono o carbono 14, un
isótopo del carbono, y estableció su vida media en 5600 años.
Este descubrimiento permitió establecer fechas de vida de organismos que
vivieron en épocas prehistóricas.Por sus hallazgos Libby obtuvo el
premio Nobel de Química en 1960 .
d) Espejos parabólicos.
Los espejos parabólicos tienen la siguiente propiedad:un rayo de luz emitido desde su foco se refleja en la dirección horizontal de su eje. Veámoslo en la figura:
Entonces
por la ley de reflexión de la luz. Además es claro que
y
Ahora,
Puesto que
de (1.1.15) obtenemos
De (1.1.16) obtenemos
La ecuación (1.1.17) la podemos escribir así:
Integramos a ambos lados de (1.1.18) y obtenemos
O también así:
De (1.1.19) obtenemos que la solución
de (1.1.17) satisface
lo cual nos indica la forma parabólica del espejo.
a). Caída Libre
Denotemos con
el espacio recorrido en el tiempo
por un cuerpo que cae libremente bajo la acción de la gravedad. Entonces
denota la constante de gravitación universal. De (1.1.1) se deduce que
es una constante. Si suponemos que en
la velocidad del cuerpo es conocida y denotada por
,
de (1.1.2) obtenemos que
es una constante. Si suponemos que en
la posición del cuerpo es conocida y denotada por
,
de (1.1.4) obtenemos
y por simplicidad
estamos ante el caso de caída libre y tendremos, por (1.1.3) y (1.1.5)
que
b) Caída con movimiento retardado.
Si suponemos que el aire ejerce una resistencia proporcional a la velocidad del cuerpo de masa
la segunda ley de Newton nos dice que
Puesto que
(1.1.8) toma la forma
,
o también así
Si suponemos que
( el cuerpo parte del reposo) (1.1.10) toma la forma
De (1.1.11) se deduce que
ésto es, la velocidad de caída tiende a
estabilizarse.c) Descomposición radactiva.
Si llamamos
la cantidad de material radiactivo que se descompone con el transcurso del
tiempo, la ecuación diferencial que rige dicha descomposición se
rige por medio del siguiente problema de valor inicial
donde
es una constante que depende del material que consideremos. El signo menos
indica que estamos ante un proceso de descomposición. Con
indicamos la cantidad de material con la que se inicia el proceso de
descomposición. La solución al problema (1.1.12) es
La vida media del material es el tiempo
necesario para que el material se reduzca a la mitad, ésto es
De (1.1.14) se deduce que
Observemos que la vida media
no depende de la cantidad inicial del material. Un gramo de plutonio y una
tonelada del mismo se reducen a su mitad en el mismo tiempo
Willard Libby descubrió en 1940 el radio carbono o carbono 14, un
isótopo del carbono, y estableció su vida media en 5600 años.
Este descubrimiento permitió establecer fechas de vida de organismos que
vivieron en épocas prehistóricas.Por sus hallazgos Libby obtuvo el
premio Nobel de Química en 1960 .d) Espejos parabólicos.
Los espejos parabólicos tienen la siguiente propiedad:un rayo de luz emitido desde su foco se refleja en la dirección horizontal de su eje. Veámoslo en la figura:
Entonces
por la ley de reflexión de la luz. Además es claro que
y
Ahora,
de (1.1.15) obtenemos
De (1.1.16) obtenemos
La ecuación (1.1.17) la podemos escribir así:
Integramos a ambos lados de (1.1.18) y obtenemos
de (1.1.17) satisface
Suscribirse a:
Entradas (Atom)